ContiTech Schwingungstechnik

Jedes Feder-Masse-System führt Schwingungsbewegungen aus, sobald es erregt wird. In der Praxis unterscheidet man zwei Arten der Erregung:

• Stoßerregung
• kontinuierliche Erregung

Wird das System durch einen Einzelstoß, z. B. beim Stanzen, aus seiner Ruhelage ausgelenkt, dann schwingt es mit seiner Eigenschwingungszahl (Eigenfrequenz) so lange, bis die dem System zugeführte Bewegungsenergie sich infolge Dämpfung in Wärme umgesetzt hat.

Wird das System kontinuierlich erregt, z. B. infolge Restunwuchten rotierender Maschinen, dann schwingt es stets mit der ihm aufgezwungenen Erregerschwingungszahl (Erregerfrequenz).

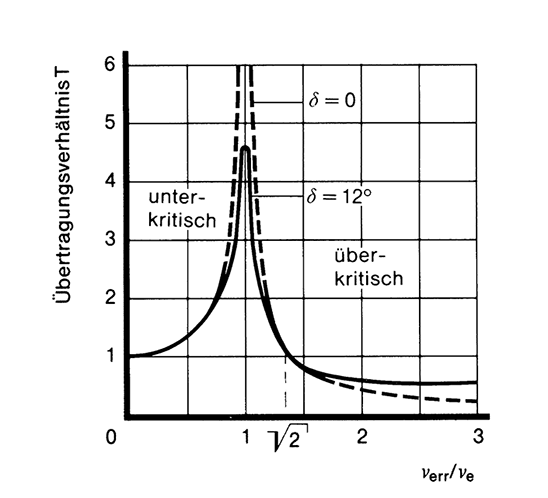
Ist die Erregerschwingungszahl gleich der Eigenschwingungszahl des Systems, dann liegt Resonanz vor. Bei nicht vorhandener Dämpfung im System würden die Schwingungsausschläge unendlich groß werden.

Die Eigenschwingungszahl eines ungedämpften Einmassenschwingers ist durch die Federrate c sowie die Größe der Masse m bestimmt. Sie errechnet sich nach folgender Formel:
$$ V_e = \frac {30}{\pi} \times \sqrt {\frac {c}{m} \times 1000} $$ $$ min^{-1}\,c \, in\,N/mm $$ $$ m\,in\,kg $$ Die Eigenfrequenz beträgt 1/60 des Wertes der Eigenschwingungszahl.
$$ f_e = \frac {1}{2 \times \pi} \times \sqrt {\frac {c}{m} \times 1000} \quad Hz $$

Für lineare Federkennlinien besteht zwischen dem statischen Federweg s – infolge der Masse m – und der Federrate c ein direkter Zusammenhang. Unter Berücksichtigung dieser Tatsache kann die Eigenschwingungszahl bzw. Eigenfrequenz bei Kenntnis des statischen Federweges nach folgenden Gleichungen bestimmt werden: $$ V_e\,\tilde{}\,\frac {300}{\sqrt{s}} \quad min^{-1}\,s\,in\,cm $$ $$ f_e\,\tilde{}\,\frac {5}{\sqrt{s}} \quad Hz\,s\,in\,cm $$ Für progressiv bzw. degressiv verlaufende Federkennlinien muß anstatt des realen Federweges s der Wert der Subtangente ssub in obige Formel eingesetzt werden.